Optimizing the Fun Away

2024-07-01 1529 words 8 min

I recently got Beltmatic, a minimalist math-themed factory game. This is how I played through it.

I got it on the Steam Summer Sale, in order to scratch the insatiable itch caused by the wait for Satisfactory 1.0. And no, I don’t want to try Factorio.

Anyway, if you haven’t checked the Steam page yet, allow me a short introduction. Basically, it’s a very casual, minimalistic grid-based factory game. You have the ability to extract numbers from nodes, transport them with belts, and use basic math operations to combine numbers into other numbers. The goal is to create and deliver different numbers to the central cube.

I knew the game is small scale, so it felt the perfect opportunity to relax on the way to 100% achievements.

Can I Optimize Yet? #

After I got the hand of the basics, I found myself following my natural instincts, optimizing the fun away ¹. One of the achievements was related to upgrades, so out of curiosity, I looked up what the speed of each upgradable component will be by the time I’m done with them.

Turns out the answer is 8 nr/s for each belt, and operations process 1 nr/s each, except for addition, which is 2 nr/s. With this knowledge in mind, coupled with the fact that this game makes it very easy to copy-paste structures, I played around and made these templates:

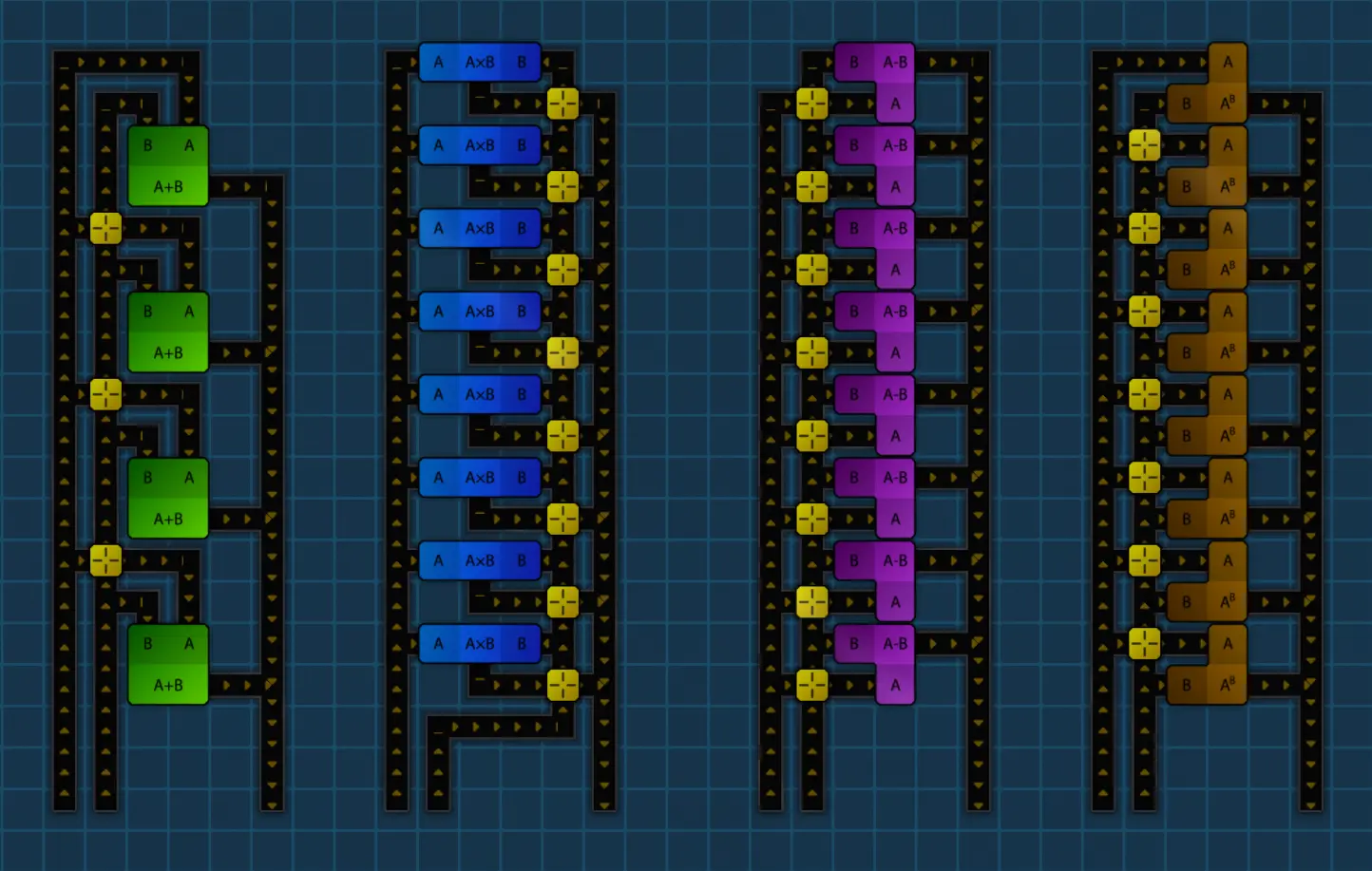
These were the building blocks of whatever I built going forward. Input and output locations clearly specified, with the same overall footprint, to be easy to tile and daisy chain.

In the early game, these won’t be efficient since the belts are way faster than the processing speed, but by the time that I would upgrade everything, the output belts should be saturated, and the input belts never stall. As I unlocked new operators, I adjusted the designs for them as well.

Armed with these, I copy-pasted my way through the early game, happily factoring the equations myself and building them quickly with these blueprint-like templates.

The Helper Tools #

Once the numbers started to reach the hundreds, it was less fun to factorize by hand, especially since you can also use additions or subtractions to give you wiggle room to reach the target number.

The next reasonable step is to ~~cheat~~ use helper tools the community made. I found this awesome little Beltmatic Calculator that does the heavy lifting of figuring out equations so that you can concentrate on building².

The nice thing is that it lets you configure what is available to use so that you don’t get solutions with operations or input numbers you haven’t unlocked yet. The results are deterministic. It seems to use A* to find the solution, so it might even be the most optimal solution.

The Factory Template #

After using the tool to help create the next few numbers for my upgrades, I noticed something that was definitely not accidental. Take a look at some examples:

1234  = (13 * 12 * 8) - 14
1337  = 15 * 15 * 6 - 13
69420 = (11 ^ 3 + 4) * 13 * 4

You will notice that as a consequence of how the algorithm works, the operations always combine the previous result with another pair of operator and input. Function composition for the win!

That is to say, mathematically you obtain the machine f(a,b,c,d) that calculates the target X from four inputs as:

X = f(a,b,c,d) = f3(f2(f1(a,b),c),d)

Of course, f1-3 are just placeholders for the binary operations +, -, * and ^ the game lets us use.

With that in mind, and with the optimal operator templates we made earlier, we can make templates for wiring diagrams. It’s easier if I lead with an example:

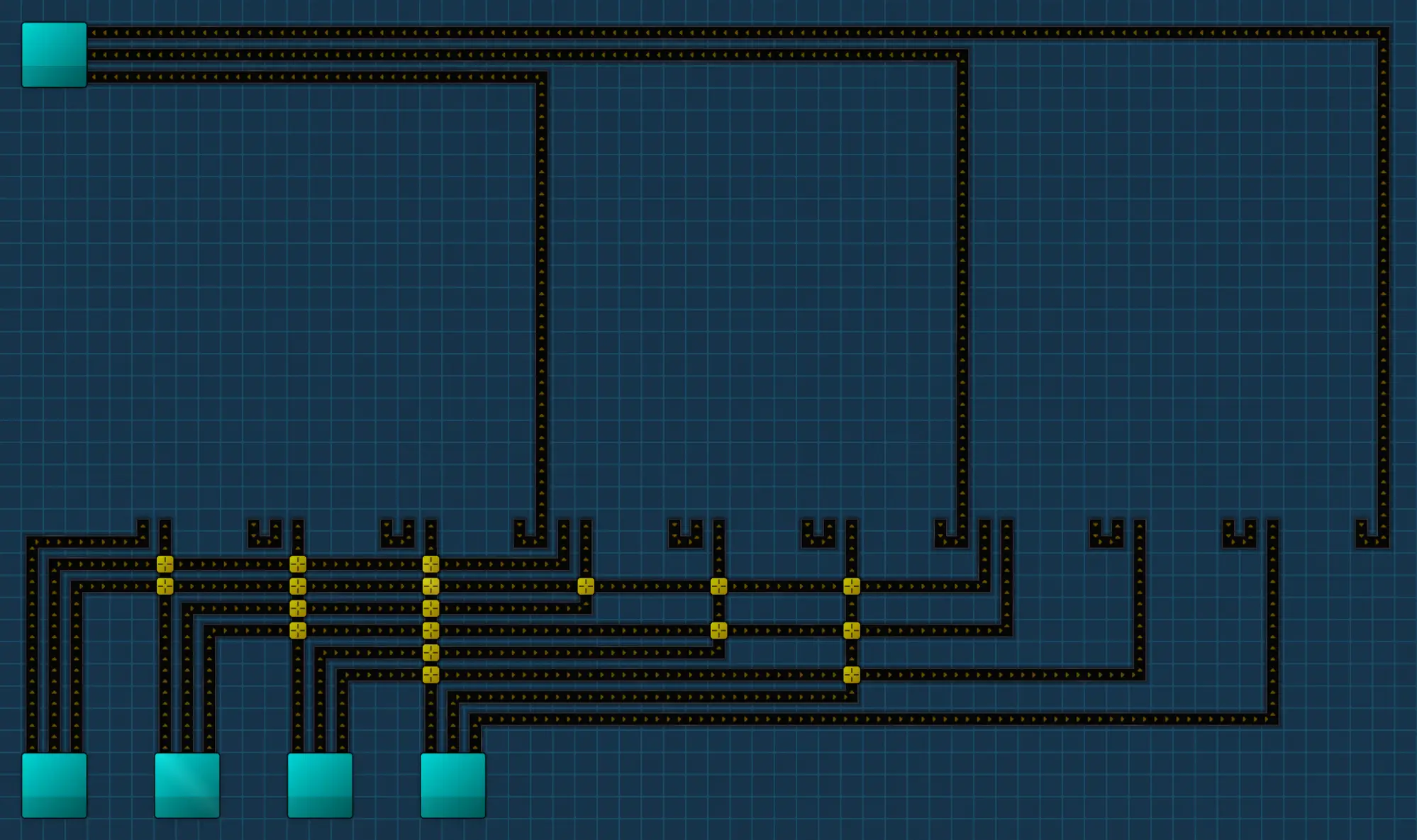
This is the wiring template for a machine that takes in four input numbers, does something and outputs a single number at the top. Note that the storage boxes are not required here; you can omit them if you haven’t unlocked them yet, but they just make for a visually pleasing indicator.

Also note that this is designed for a three belt wide bus, so we have the sweet spot between delivering at a reasonable volume and keeping the belt spaghetti manageable.

The spacing is deliberate so that we may use the modules from earlier! Let’s see an example of a machine that computes:

f(a,b,c,d) = (a + b) * c - d

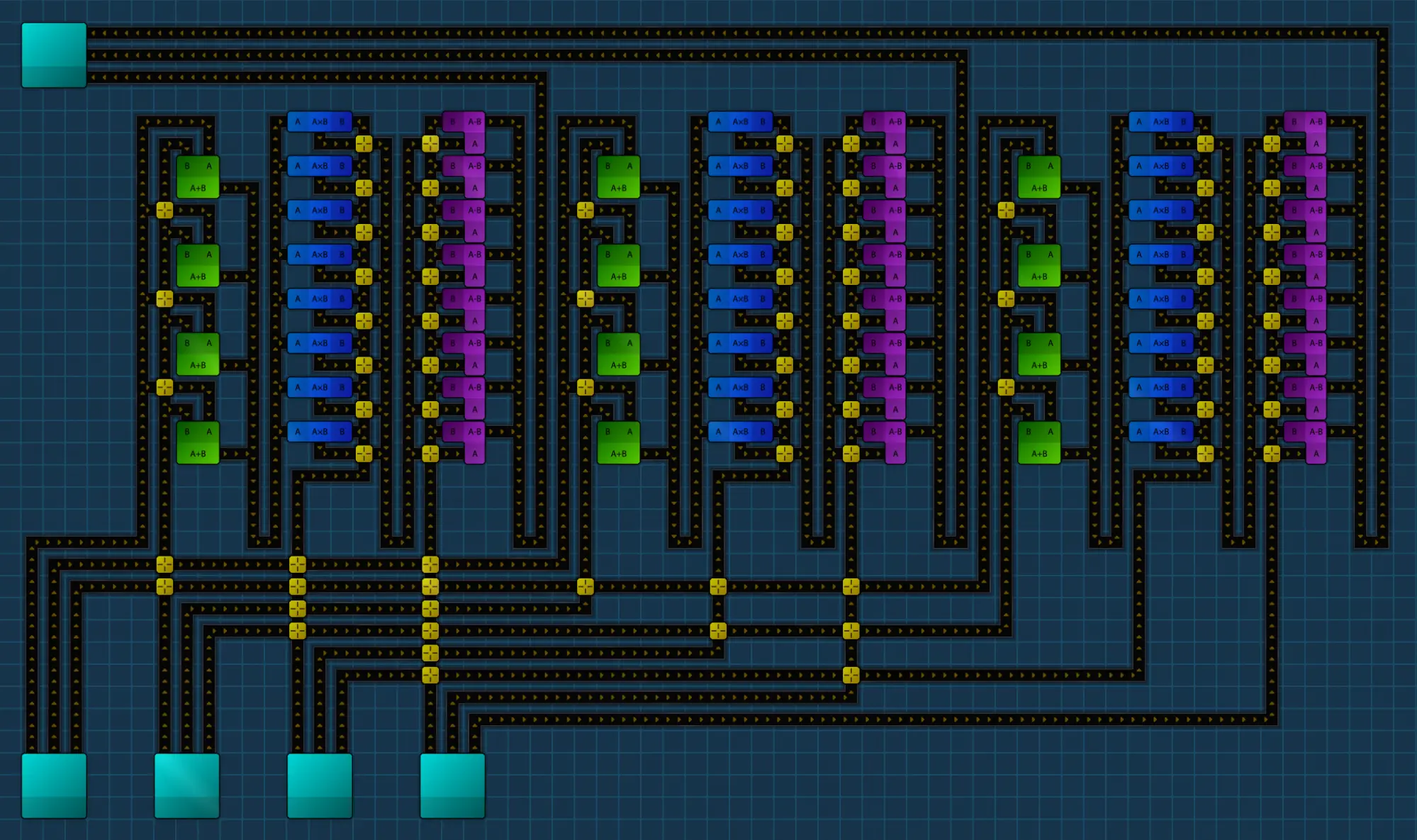
As a programmer, I think of these machines as higher-order functions: we take previous functions (our compute units) and plug them into this new function (the wiring diagram) to compute something! Or, since this game looks similar to electronics (kinda?) we can think of them as little black boxes that implement our function as a hardware abstraction at a circuit level. Anyway, the point is we can keep this machine copy-pasted somewhere, label it for what it does, and any time we need the same operations in the same order, we can reuse it!

The above example was for operations with an arity of four, you can easily extrapolate to make variants for any number of inputs you wish. I didn’t find anything that needed more than six inputs in my playthrough.

The MAM #

So, we have a very easy way of quickly building machines using copy-paste technology at our fingertips. Now what? The next obvious step is to create a machine that could output any number (hence the name: The Make Anything Machine) without the need to build anything else.

The trick we are going to use here is that you can write any number by decomposing it into powers of ten. For example:

12345 = 1 * 10^4 + 2 * 10^3 + 3 * 10^2 + 4 * 10 + 5

Now that looks rather straightforward and something we can modularize. Of course, this is not an original idea, the Beltmatic subreddit is filled with these, but the first one I saw and what inspired me to build it in my game was a user guide on Steam³. I really enjoyed their solution for digit selection, so I kept it, but built everything else from scratch.

Let’s take a closer look at how digit selection works:

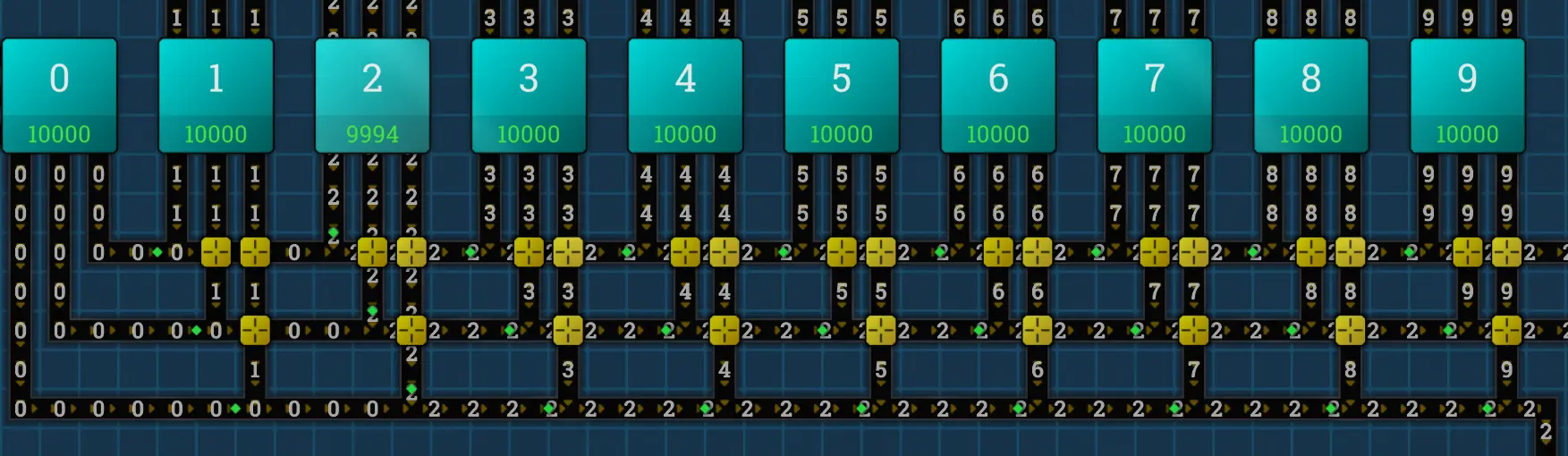
We have this contraption, that defaults to a stream of zeroes. All other digits intersect this stream, but have priority indicators preferring the main line. The trick is that in order to select a digit, we make the priority be the incoming digit, like we did with the 2 above. The only constraint this imposes is that the digit belts are always saturated. Gaps in the zero stream would cause the priority to be ignored and other digits to squeeze through.

The Units #

The units module for our MAM is the easiest to make, it’s just the digit selection. All we need is to feed in any number and subtract it from itself in order to create the zero, and bring in all the other digits from sources scattered around the map.

We end up with this:

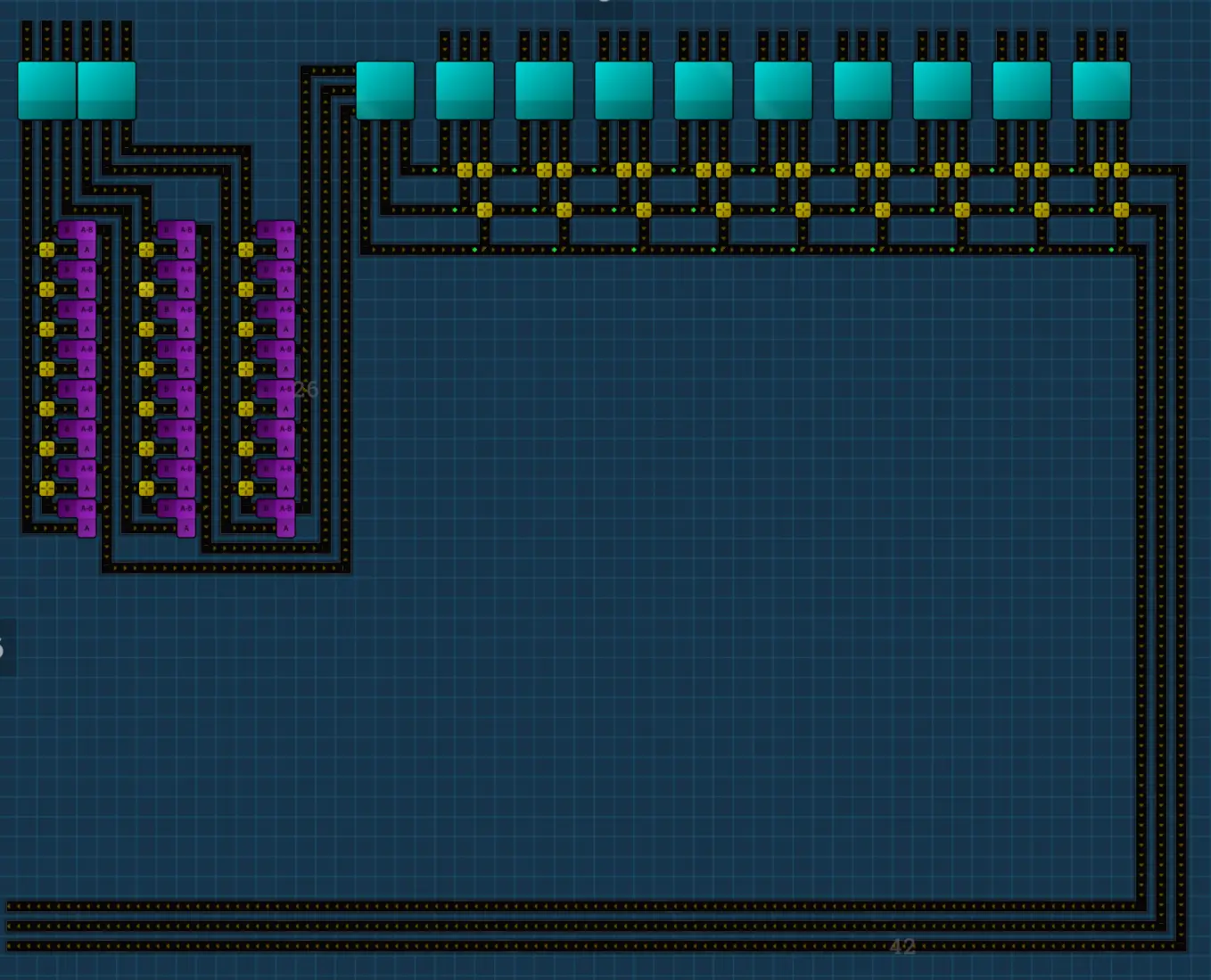
The extra space? That’s just to make it look pretty, we will add more stuff in the other modules.

The Tens #

For the tens module, we need to add a multiplication by ten. To do this, we bring in another two sets of the digit five, and create the ten with 5 + 5 = 10. Multiplying that by our selected digit, we get the tens we need. Of course, this should be added to the result of the previous module.

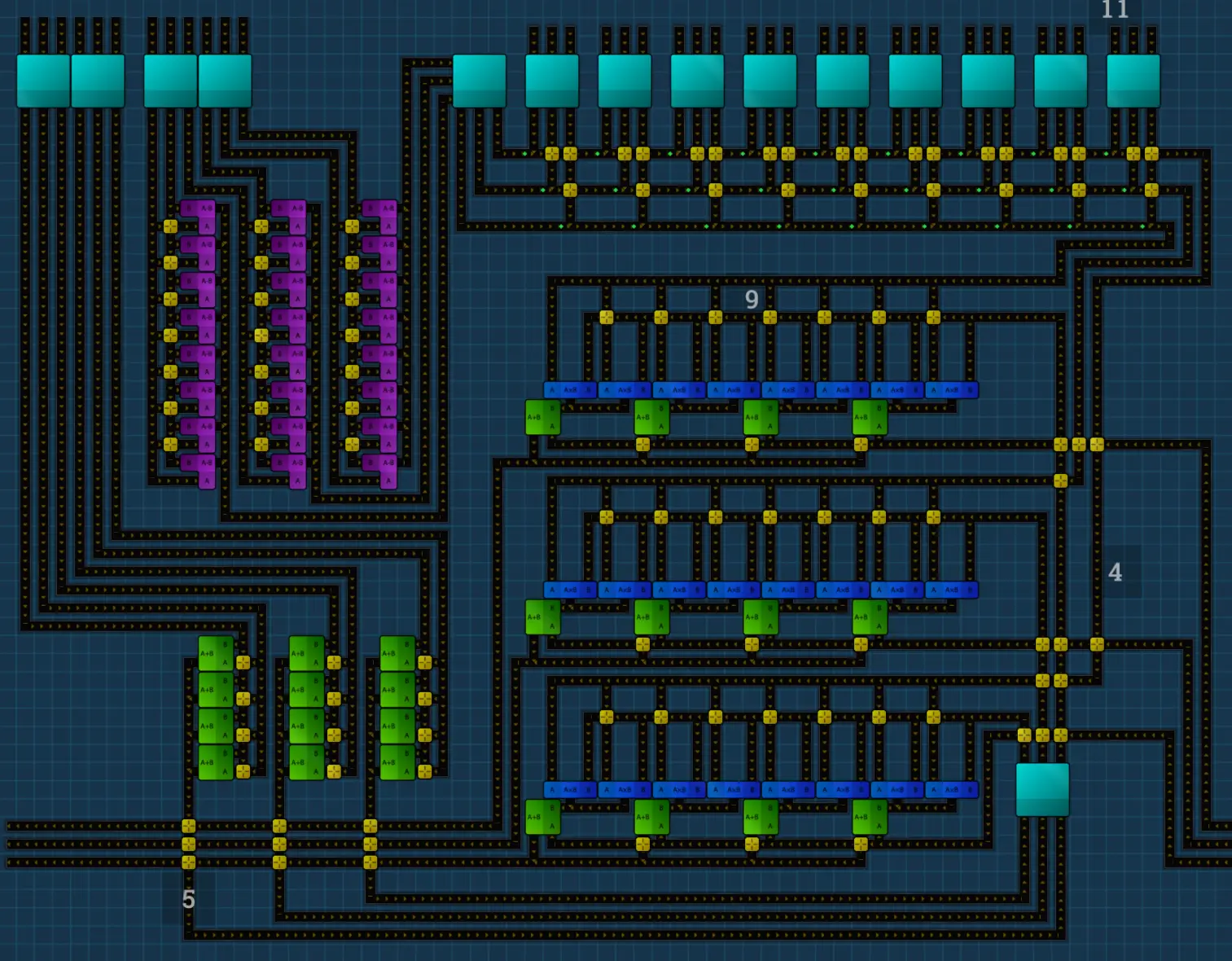
The Nths #

And now we get into what I like to call generic territory, where we calculate the n-th digit. All we need to do is also provide an exponent for the ten, which was omitted in the previous step because it was redundant.

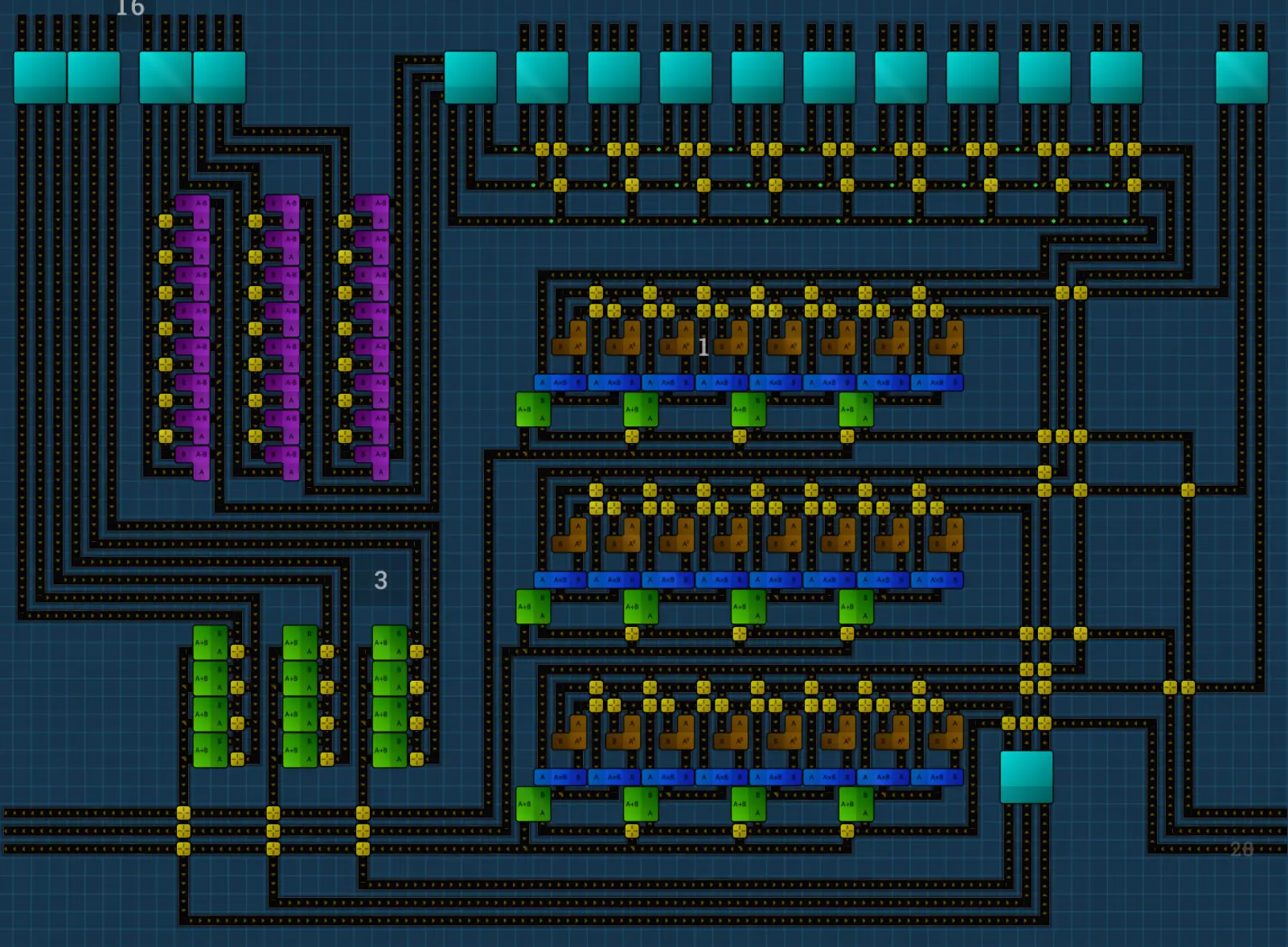
Putting Them Together #

We can now see how these modules stack, we have a manifold-like structure, meant to be built one next to the other, with the bottom bus being used as an accumulator.

This machine can now produce any four-digit number:

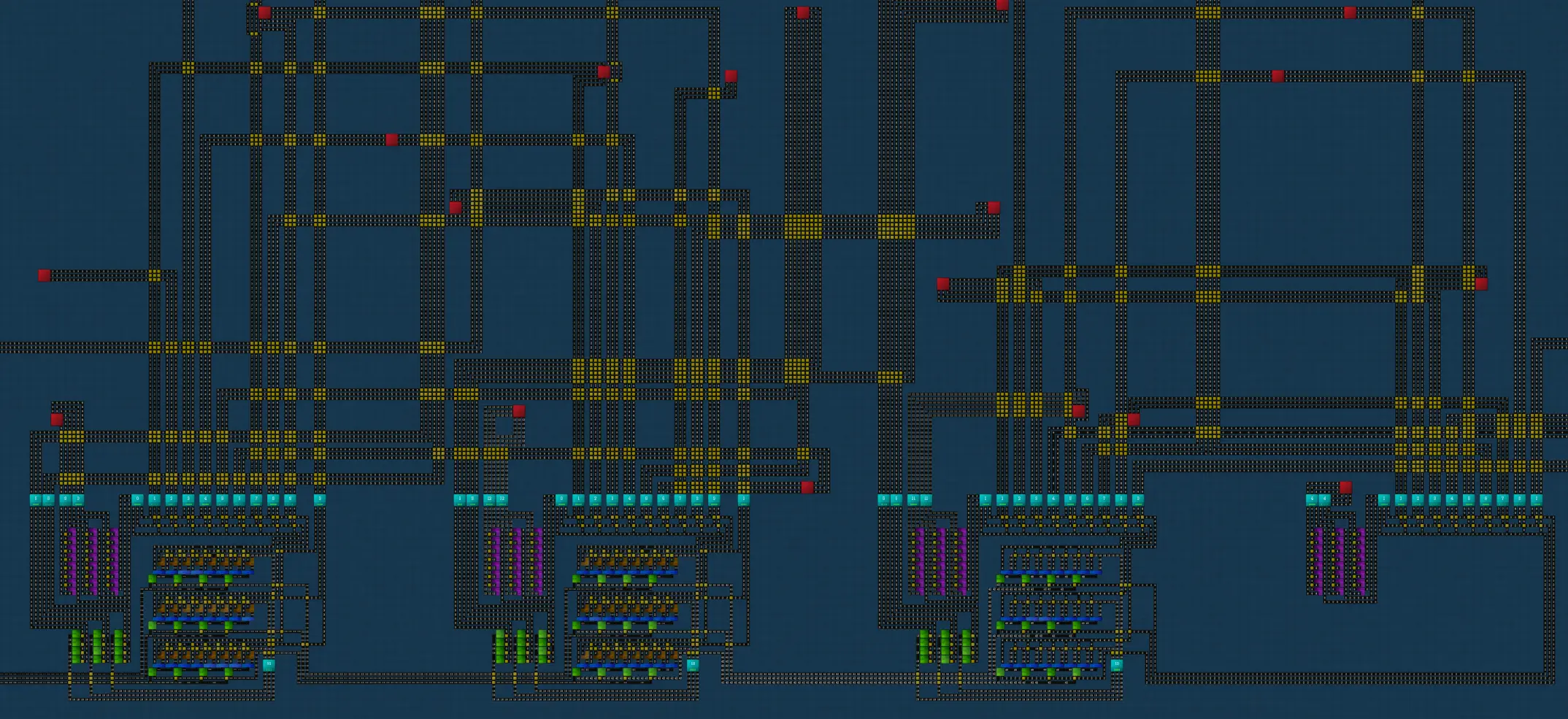
In order to 100% the Steam achievements for the game, you only require five digits. The game goes on after that, and since it stores the numbers as 32-bit signed integers, in order to create any conceivable (positive) number, we need ten digits. Anything above 2,147,483,647 will cause an overflow.

There’s a lot of spaghetti getting every input required, but all that hard work means we never have to build anything ever again!

Some notes:

The flow of digits goes from right-to-left because I built the MAM to the right of the big blue sink and I want minimum extra travel to make number switching faster. You can very easily mirror everything if you want to place it in different configurations.
The MAM presented uses three belts worth because they work well paired with the storage blocks, and a single belt would be very slow.
This MAM only outputs 24 numbers per second. You probably want to use it for the big upgrade numbers while you build smaller machines for the shorter numbers. Or… build multiple MAMs!

Category: gaming